9.1 Offerta di lavoro

La nostra teoria delle scelte di consumo ipotizza che nel compiere tali scelte gli individui prendano il loro reddito per dato. In realtà il reddito di un individuo dipende in gran parte dalle sue scelte, e in particolare dalle sue scelte di lavoro, ovvero quanto del suo tempo vendere a chi lo domanda (le imprese, come vedremo nella prossima sezione). Fortunatamente, per analizzare tali scelte non abbiamo bisogno di una nuova teoria. Come ora vedremo, l’offerta di lavoro si può infatti analizzare studiando la domanda di tempo libero.

Vincolo di bilancio del consumatore / lavoratore

Consideriamo un consumatore / lavoratore che deve scegliere quanto tempo libero trascorrere (e quindi quanto lavorare) e quanto consumare di un generico bene di consumo. Indichiamo con $T$ il tempo a disposizione (per es. 7 giorni a settimana), con $N$ il tempo libero ($0\leq N\leq T$), e con $C$ la quantità del bene di consumo. L’obiettivo dell’individuo è massimizzare la propria utilità $U(N,C)$ dato il suo vincolo di bilancio. Per capire com’è fatto quest’ultimo, indichiamo con $P$ il prezzo del bene di consumo, con $W$ il salario giornaliero, e con $M_0$ il reddito non da lavoro dell’individuo. La spesa per consumi è quindi $PC$, mentre il reddito è $M_0+WL$, dove $L=T-N$ indica le giornate di lavoro. Il vincolo di bilancio è dunque dato da

\(\begin{gathered} PC = M_0 + W \times \underbrace{(T-N)}_{L} \end{gathered}\)

Scelta ottima e funzione di offerta di lavoro individuale

Il lavoratore decide come ripartire il proprio tempo tra lavoro e tempo libero, sapendo che più tempo dedicato al lavoro significa meno tempo libero ma anche più reddito (e quindi più consumo), in base alle proprie preferenze e al vincolo di bilancio. Con preferenze del tipo Cobb–Douglas

\(\begin{gathered} U(N,C) = N^\alpha C^\beta \end{gathered}\)

l’ottimo è spesso una soluzione interna: l’individuo sceglie di lavorare un certo numero di giornate e di conservare una parte del tempo per sé. Infatti con preferenze di questo tipo l’utilità è nulla se uno dei due beni è assente, quindi il lavoratore ha convenienza a consumare entrambi.

Tuttavia, anche Dalla nostra analisi delle scelte di consumo (Capitolo 2) dovrebbe essere chiaro che, anche se il reddito non da lavoro è pari a zero, e quindi il vincolo di bilancio tocca l’asse orizzontale, la soluzione d’angolo con $N=T$ è possibile (così come è possibile quella con $N=0$) se la funzione di utilità del lavoratore è $U(N,C) = (N+\sigma)^\alpha (C+\sigma)^\beta$ con $\sigma>0$. con preferenze Cobb–Douglas può verificarsi una soluzione d’angolo dove l’individuo non lavora affatto. Se il reddito non da lavoro $M_0$ è sufficientemente alto e il salario reale $W/P$ sufficientemente basso, lavorare diventa poco conveniente: l’individuo preferisce non partecipare al mercato del lavoro, scegliendo $N=T$.

La figura seguente mostra come varia la scelta ottima di tempo libero e consumo al variare dei parametri della funzione di utilità ($\alpha$ e $\beta$), del reddito non da lavoro $M_0$, del salario $W$, e del prezzo del consumo $P$.

È importante 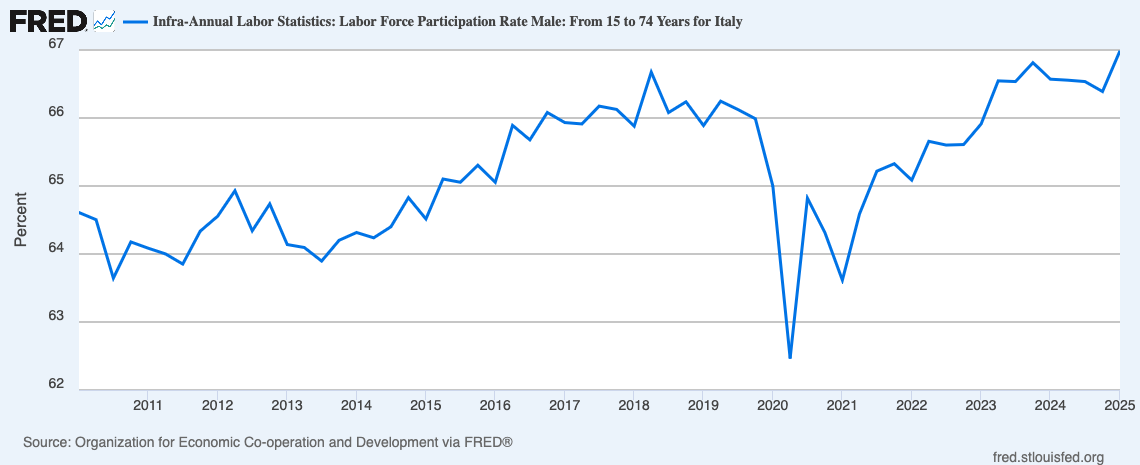In Italia, la partecipazione alla forza lavoro è cresciuta dal 61% circa del 2010 al 67% circa del 2025. sottolineare che un’offerta di lavoro nulla non equivale alla disoccupazione del lavoratore, ma alla sua non partecipazione alla forza lavoro: l’individuo sceglie volontariamente di non lavorare. La disoccupazione involontaria — cioè il caso di chi vorrebbe lavorare al salario di mercato ma non trova impiego — non può verificarsi in equilibrio, che il mercato sia concorrenziale o, come vedremo, caratterizzato da potere di mercato dal lato della domanda. Nella realtà, ovviamente, la disoccupazione esiste eccome, e in Italia ha storicamente livelli particolarmente alti. Solo interventi esterni, come ad esempio un salario minimo fissato al di sopra del livello di equilibrio, possono creare disoccupazione involontaria.

Funzione di offerta di lavoro di mercato

Come accade per la funzione di offerta di qualunque altro bene, anche la funzione di offerta di lavoro nell’intero mercato è semplicemente la somma orizzontale delle funzioni di offerta di lavoro dei singoli lavoratori. La seguente figura rappresenta l’offerta di lavoro corrispondente a una popolazione di lavoratori identici, ciascuno caratterizzato dalla funzione di utilità $U(N,C)=NC^2$.