9.2 Domanda ed equilibrio nei mercati del lavoro concorrenziali

Nel Capitolo 8 abbiamo analizzato la massimizzazione del profitto di un’impresa concorrenziale. Nel breve periodo, la scelta ottima dell’impresa è Nel lungo periodo, se i costi fissi sono sufficientemente bassi allora la regola di massimizzazione del profitto è la stessa; se invece non lo sono, la scelta ottima è invece chiudere l’impresa. produrre al livello di output in corrispondenza del quale il costo marginale è pari al prezzo di vendita dell’output: $MC=P$.

Dato che output prodotto, $Q$, e lavoro impiegato, $L$, sono variabili legate in maniera univoca dalla funzione di produzione dall’impresa, $Q=F(L)$, un modo equivalente di procedere è calcolare la quantità di input che massimizza il profitto dell’impresa.

Domanda individuale di lavoro

Anziché invertire la funzione di produzione e scrivere quindi sia costi che ricavi in funzione della quantità di output $Q$, possiamo scrivere costi e ricavi in funzione della quantità di lavoro impiegata, $L$, in questo modo:

\(\begin{gathered} C = FC + WL \end{gathered}\)

\(\begin{gathered} R = P\times F(L) \end{gathered}\)

Nel breve periodo, la quantità di lavoro ottimale per l’impresa è quella che massimizza la differenza $R-C$. All’aumentare del livello di impiego del fattore lavoro, $L$, il costo dell’impresa aumenta ad un tasso pari alla sua derivata rispetto a $L$, che chiameremo costo marginale del lavoro (Marginal Labor Cost) e che, per un’impresa concorrenziale, è semplicemente il salario:

\(\begin{gathered} MLC = \frac{dC}{dL} = W. \end{gathered}\)

Analogamente, il ricavo dell’impresa aumenta ad un tasso pari alla sua derivata rispetto a $L$, che chiameremo ricavo marginale del lavoro (Marginal Labor Revenue), dato dal valore in euro del prodotto marginale del lavoro:

\(\begin{gathered} MLR = P\times \frac{dF(L)}{dL}=P\times MP_L \end{gathered}\)

Il livello di impiego di lavoro che massimizza il profitto dell’impresa è quello in corrispondenza del quale si ha $MLR=MLC$:

\(\begin{gathered} P\times MP_L = W \end{gathered}\)

In altre parole, per massimizzare il profitto nel breve periodo, Conoscevamo già questa regola. Ricordando che $MC=W/MP_L$ è facile vedere che l’equazione non è altro che $MC=P$. l’impresa impiegherà lavoro fino al livello in corrispondenza del quale il ricavo derivante dall’impiego di un’unità aggiuntiva di lavoro è pari al suo costo.

Se fissiamo il prezzo del bene prodotto dall’impresa, $P$, le uniche due variabili nell’equazione sono il prezzo e la quantità di lavoro, ovvero $W$ e $L$. L’equazione descrive quindi la funzione di domanda di lavoro (di breve periodo) dell’impresa: data la tecnologia $Q=F(L)$ e il prezzo $P$ del bene prodotto, la funzione associa ad ogni possibile livello di salario $W$ la quantità di lavoro $L$ che massimizza il profitto dell’impresa.

Riprendiamo ancora una volta l’esempio che abbiamo sviluppato nel Capitolo 7 e nel Capitolo 8, dove la funzione di produzione dell’impresa è $Q=F(L)=80\sqrt{L}$. Supponiamo che il prezzo del bene prodotto sia $P=2,50$. Il profitto dell’impresa è allora

\(\begin{gathered} 2,50\times 80\sqrt{L} -WL \end{gathered}\)

Ponendo la derivata rispetto a $L$ pari a zero (ovvero uguagliando il ricavo marginale del lavoro $MLR=2,50\times 80/(2\sqrt{L})$ al costo marginale del lavoro $MLC=W$) otteniamo la funzione di domanda inversa di lavoro dell’impresa

\(\begin{gathered} W=\frac{2,50\times 80}{2\sqrt{L}} \end{gathered}\)

La funzione di domanda di lavoro dell’impresa è quindi

\(\begin{gathered} L = \frac{10000}{W^2} \end{gathered}\)

Per esempio, Sapevamo già che quando $W=64$ e $P=2,50$, la scelta ottima di breve periodo dell’impresa è produrre $Q=125$ unità di output, come risulta per es. dalla Figura 8.3 e dalla Figura 8.6. se il salario è $W=64$, la quantità di lavoro domandata dall’impresa è $L=10000/64^2$, e quindi la quantità di output offerta dall’impresa è $Q=80\sqrt{10000/64^2}=125$.

Il grafico qui sotto illustra l’esempio che abbiamo appena discusso. Nel grafico è anche possibile vedere come la funzione di domanda di lavoro varia al variare della produttività (parametro $A$) e del prezzo dell’output (parametro $P$).

Domanda di lavoro nel mercato

La domanda di lavoro dell’intero mercato si ottiene sommando orizzontalmente le domande delle singole imprese, come illustriamo nella figura seguente. A ogni livello di salario, consideriamo quante unità di lavoro ciascuna impresa vuole impiegare, e le sommiamo. La curva di domanda di mercato dipende dalla tecnologia delle imprese, dal prezzo dell’output, e dal numero di imprese operanti nel mercato. In particolare, se il prezzo dell’output aumenta, la curva di domanda di lavoro di ogni impresa si sposta verso destra, e di conseguenza anche quella di mercato si sposta verso destra. Analogamente, un aumento del numero di imprese produce un’espansione della domanda complessiva di lavoro.

Equilibrio concorrenziale

L’equilibrio concorrenziale nel mercato del lavoro si determina, come in tutti i mercati, dall’intersezione fra domanda e offerta. Il salario di equilibrio è quello al quale la quantità di lavoro che le imprese desiderano assumere è esattamente uguale alla quantità di lavoro che i lavoratori desiderano offrire. E come in ogni altro mercato concorrenziale, l’allocazione di equilibrio è socialmente efficiente: le unità di lavoro che valgono per le imprese più del salario vengono impiegate, e i lavoratori disposti ad accettare quel salario trovano impiego.

Nel modello di concorrenza perfetta, l’equilibrio assicura quindi piena occupazione (compatibilmente con l’offerta) e nessun surplus lasciato irrealizzato: il surplus totale (somma del surplus dei lavoratori e delle imprese) è massimo.

Salario minimo

Cosa 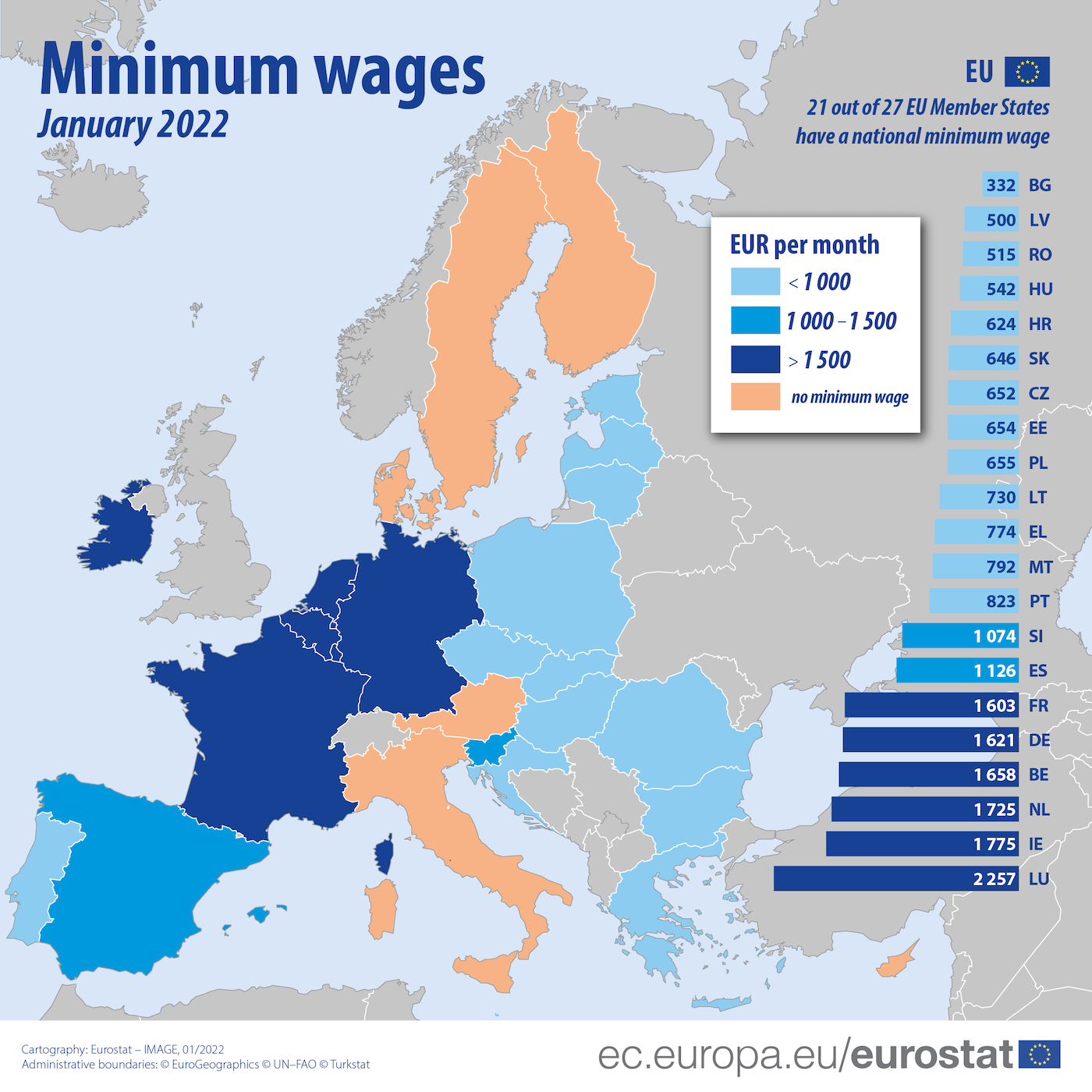In Europa la maggior parte dei Paesi ha un salario minimo legale, con livelli diversi. In Italia invece non esiste un salario minimo: la tutela dei salari è affidata ai contratti collettivi, ma il tema è oggetto di dibattito politico. accade se lo Stato introduce un salario minimo, cioè un livello $W_\text{min}$ al di sotto del quale non è consentito stipulare contratti di lavoro?

È facile vedere che se $W_\text{min}$ è più basso del salario di equilibrio, non ha alcun effetto: il mercato continua a operare al punto di equilibrio originario. Se invece $W_\text{min}$ è più alto del salario di equilibrio, la quantità di lavoro offerta dai lavoratori aumenta, mentre la quantità domandata dalle imprese diminuisce. Ne risulta un eccesso di offerta di lavoro, cioè disoccupazione involontaria, e una perdita secca di benessere rispetto all’assenza di interventi.

Questo risultato rappresenta la previsione standard del modello di concorrenza perfetta: il salario minimo riduce l’occupazione e l’efficienza del mercato. Tuttavia, come vedremo nella sezione successiva, se il mercato del lavoro non è concorrenziale dal lato della domanda — cioè se chi compra, ovvero le imprese, hanno potere di mercato — l’effetto cambia radicalmente: in quel caso, il salario minimo può aumentare l’occupazione e ridurre la perdita secca.